This is a answer I gave on quora to this question: Do any non-linear dynamic (chaos theory) equations describe user growth in lean startups?
I am going to generalize my answer to technology startups, but the concepts can be abstracted to most startups.
Introduction:
Forgetting the complex equations, lets try and make a function where only technology development and business development (for simplicity) are inputs and get user growth as an output. If the system was linear then the more technology and the more business which goes into the company would result in more users.
But in real life, user acquisition is more complex than this: Not all tech and business development is the same and company change and pivot and users come in cycles, not linearly. There are competitors in the market and fundamental changes in technology. All of these will contribute to the user growth in a startup.
Now lets bring in a non-linear dynamic systems model: taking the technology adoption lifecycle and constant product iteration into the picture. If we still use the tech and business development to shows user growth, but describe the function as a chaotic system, then small changes in tech and business development results in very different user growth making the full system unpredictable.
That is how chaos theory describes user grown in startups!
Read the full explanation for more details with a specific strange attractor model:
Prerequisites:
- Understand Technology Adoption Lifecycle
- Understand the Pivot in terms of Lean Startups
- Non-linear equations, chaos theory and strange attractors
- Rössler attractor model for non-linear dynamic user growth in startups
1. Technolgy Adoption Lifecycle
If you have read Geoffrey Moore’s Crossing the Chasm he describes the technology/innovation adoption lifecycle in detail as following a normal distribution or bell curve:
2. The Pivot
Now if you have read Running Lean by Ash Maurya, The Lean Startup by Eric Ries or The Startup Owner’s Manual by Steve Blank you will learn about the pivot.
The pivot is a “structured course correction designed to test a new fundamental hypothesis about the product, strategy, and engine of growth.” Steve Blank defines a pivot as “changing (or even firing) the plan instead of the executive (the sales exec, marketing or even the CEO).” The main idea behind the pivot is after building a minimal viable product (MVP) and testing it in the market, you take the feedback you got from launching the early prototype to understanding the market to hopefully finding better product-market fit in the next interation.
A great example of a pivot used by a company was Groupon; when the company first started, it was an online activism platform called The Point. After receiving almost no traction, the founders opened a Wordpress blog and launched their first coupon promotion for a pizzeria located in their building lobby. Although they only received 20 redemptions, the founders realized that their idea was significant, and had successfully empowered people to coordinate group action in purchasing. Three years later, Groupon would grow into a billion dollar business.
3. Non-linear equations, chaos theory and strange attractors
To understand the concepts better, you can read the answer to this question: Briefly, what is chaos theory? but I will summarize it here.
When Newton invented calculus, scientists and methematicains were able to derive “dynamic models” of real world physical systems. For example you can model and predict the trajectory of a canon on earth (assuming no wind) very accurately since it follows a curve determined by an ordinary differential equation that is derived from Newton’s second law.
By understanding the initial position of the canon, its initial velocity and the acceleration force of gravity we can predict where it will land. Even if the measurement of initial conditions are slightly incorrect, the prediction will be very close to the actual trajectory (within a couple feet/meters lets say). But what if there is no linear equation which can govern the motion? Let’s enter the world of Chaos Theory.
In a chaotic dynamical system, a small change in initial conditions will lead to a qualitatively different behaviour. A great example is weather. Choas theory was discovered by Edward Lorenz when he was making weather predictions. He used sample data of initial weather conditions (beginning of the week) to simulate future weather conditions for a week. When he did this a second time, he thought it might take too long to start from the beginning of the week so he started from the middle. What he found was that the predictions from the starting conditions of the week were very different to those that were the outcome of the conditions at the middle of the week.
This system is still deterministic; if you are able to reproduce the initial conditions exactly, it will follow the same behaviour over and over again. However, slight perturbations of the initial conditions lead to very different trajectories.
Now take the animation below.
Let’s say a simple equation when plotted at a certain point of time looked like the following:
What is unique is that the line goes back upon itself. At one instant you are at the top right left (Figure above), the next you are at the bottom right (figure below)
If the top left represented sunny, hot and humid and bottom right represented cloudy, cold and dry, what makes the system chaotic is that a small change in the input would result in a very different output. For example, a change of 0.5 in the current temperature reading after 6 time periods for example shown in the figure blow would be a completely different forecast (hot and humid vs dry and cold) and a seemly random output. This is the so called “butterfly effect”.
If the dynamic system model evolves through phase space in a way which appears to repeat (called a Fractal in mathematics), then the system of equations which describes its motion can be described a Strange Attractor (there is a more formal mathematical definition, unnecessary for this explanation).
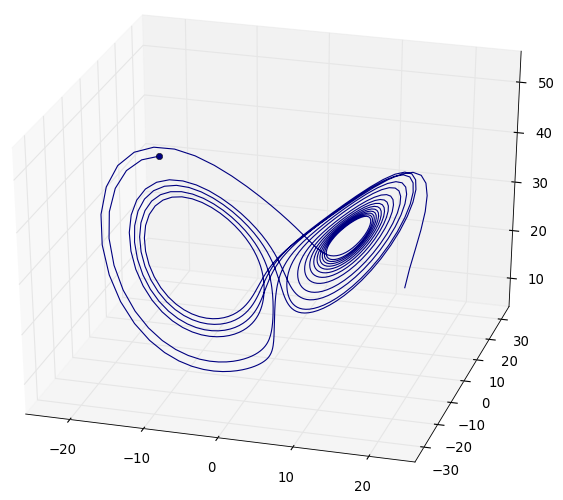
4. Combining the concepts 1 and 2 to form the Rössler Attractor Model**
So if you combine the technology adoption cycle with the idea of a pivot, every-time a startup company pivots, their company/product has a new addressable market and follows a the bell curve described by the technology adoption lifecycle.
This can be modeled using a Rössler attractor shown below to described the non-linear dynamic user growth in startups.
You can think of the z axis as user acquisition, and the x and y axis as technology and business development. After putting in some initial tech and business development, when a startup their first MVP, then have a certain adressable market where they are able to get customers. This can be seen by a curve describing the small jump in user acquisition. As companies iteratate their product, their user aquistion will (ideally) increase as described by the model.
Realistically though, in one iteration of the pivot, only part of the technology development cycle will be reached so in reality the model describing real life user acquisition would be much more complex variation of the Rössler attractor.
The point is that with very small changes in the technology development (a specific bug or feature) or business development (one sales deal or one marketing campaign which goes viral), there would be an unpredictable change in user acquisition (as modelled in this example).
Also of note, most people talk about the butterfly effect or chaos theory as a sort of a misnomer. It isn’t “small changes will cause large effects” but Chaos is more actually “small changes lead to unpredictability”. So if user acquisition can be modelled with a strange attractor such as the Rössler attractor, what the model is saying is that it is practically impossible to predict/model the success of a startup (or use growth) even if you have full control on the technology and business development.
Hope this makes sense!
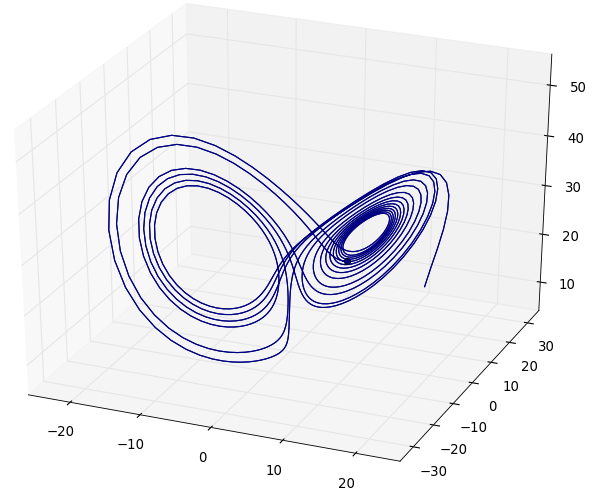
For fun here is a nice render of the Rössler attractor.
